The quote seems easy enough. Lefort is right in rejecting Marx's theory of class difference while accepting the validity of early Marx's societal observations, and we see the re-emergence of reification here. What might not seem so obvious is that it's a reification of one's very self for some sort of value (something which, as Lefort notices, also happens in Communism's totalizing idealism in almost the exact same manner, one for a single symbolic value, the other for one symbolic value (determined by the probability signified by the number) out of many), something far different than the commodity fetishism addressed by Marx. However, this is not the place to unpack this, as there's a rather more difficult question that demands answering first.
I've got to deal with another problem here, one that Lefort doesn't even recognize and skips over with almost
Namely, why is "networks" plural?
First, let us register suprise: on one side of the equation, we have a single body, a citizen (the organ of society, the organ of the publicity), and on the other side, mutliple… locations? What exactly is a network? And why are there so many of them?
Let's start with a very basic definition: a network is a linked series of independent actors (nodes), each one passing output to another node, which takes that output, runs some process on it (which of course, can be determined by the data type or information within the data), and then generates new output, either directed to the first node or an entirely new one. These actors are not "joined," necessarily, but they are "related." This information eventually passes through the entire network depending on the functions of interactions behind nodes and the original output passed in. The behavior of these networks tends to follow rather odd statistical properties.
In use, it's assumed that each network fully contains all of its actors (i.e. there is only a single network in the problem), and that all of these actors are of the same type. For example, in neural network modeling, each node represents a neuron, and every node has the same behaviors. After all, each node is contained in the network of that particular area of the brain, and is always passed the same functions which undergo the same set of internal interactions; how could they evolve new properties, new mechanics if there's no source of new?
To proceed to the problem of n number of networks, I need to discuss two things. First, Schrodinger's equation. The equation:
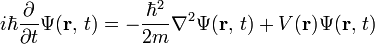
While I'll pass over the rather complex details of the equation itself, I'd like to focus on one particular behavior generated by this equation. When multiple wavefunctions are superposed on a single particle, the probability function suddenly becomes time dependent; the actual wavefunction of the particle, the function describing the probability of the particle's location shifts and changes, peaks rising and falling until they reach their starting position, at which point they repeat the cycle all over again.
Second, Systems theory (be warned: I think I'm right in what I say here, but it could be complete bullshit. proceed with caution). A system is a lot like a network; however, where the relation between nodes in a network is often viewed as communicative, incorporeal, lightly abstract, each node retaining its own individual identity, preventing the network from becoming a fully closed body (but not quite; thinking of a network as Deleuze's BwO is more than a bit problematic). Systems, however, eat the parts constructing it to produce some sort of greater body. Ecological systems all have very real interactions occurring between parts; they eat, shit, and fuck one another, constructing the greater body of the ecosystem (forest, ocean, tundra, etc.). Social systems often follow the flow of risk and reward, concrete connections. Organizational Theory subsumes the worker (informational or physical) within the organization at large.
So, in Lefort's construction (which I happen to agree with, for reasons I probably don't have the time to go over here), humans are actors in network*s*. Within each one of these networks, the individual outputs information, and receives transformed output from connected actors, who also pass the output onwards. But, what exactly is at the space connecting these networks, and what sort of result does it have? By connecting these networks together at the site of the body, we have (in effect, due to the same logic as the time-dependent Schrodinger equation) created a time-dependent system, constantly shifting through new sets of probabilities, constantly in flux until the moment of measurement (if you don't understand why I'm calling this a system after somewhat opposing systems and networks earlier, think of it this way: the social/political system is a system whose parts are networks). So, we've found the source of the flux described by so many. But, we have suddenly found a new problem:
If the individual defines themselves in the space of terms passed to them by their community, what happens to this self-definition when one finds themselves in multiple communities/networks? In other words, the problem isn't mere reification; it's a much deeper ideological dissonance that constantly tears the very ego, the very self apart.
At this point, I was thinking I'd mention the work of James Bohman, but getting through all of that took far longer than I thought it would. I also thought I'd bring up the Nietzschian element of the "time-dependent network system," but couldn't really think of it (the looping nature of Schrodinger equation makes it a bit like the eternal return). For those that have struggled through this: thanks for putting up with my bs and/or attempt to both complete an assignment and attempt to define my major at once. To Chun: can you please tell me how much of the Systems Theory stuff I've got right when we meet next week?
No comments:
Post a Comment