 Cosmopolitans need to start thinking about the speed of light
Cosmopolitans need to start thinking about the speed of lightThere are a number of series/expansions in mathematics which transform a function into an infinite sum of increasingly shrinking terms. However, as Leibnitz observed, the human mind cannot handle infinity (or, rather, possess the capability of movement required to compute the terms of an infinite set, make them concrete, within the limits placed by our own lives and haunted by Cantor's Diagonality Theorem), and thus has to reduce. This leads to two collararies dictating the use of Taylor Series:
(from Wikipedia)

Which has an error of about 0.000003. So it's essentially right.
But why exactly would you need it? What's the use in disintegrating a function and letting it dissolve off into infinity? A good number of things, actually. The case above can be used to prove various corollaries of wave theory, often using the Taylor series of cos(x) (which just fills in the missing elements of sin(x)). Other such examples abound.
In a certain sense, this is the very problem Appadurai is attempting to grapple with; since (following Derrida) meaning is infinitely vanishing, infinitely deferred (differentiable?), Appadurai must throw out the concrete notions of space and identity propagated by Anthropology and attempt to factor in movement (which is possibly not even movement at all?). Whatever new function he derives is ineffable, infinite, so it must be broken into parts (an approximation) to be made sense of, to feed in to other theoretical processes and actions. Leading to the -scapes. However, at this point we encounter a new problem: all of these -scapes contain the same origin function. Delineating them as clearly different spaces/fields, as the naming/encapsulating process usually does, quickly becomes a problem when one attempts to locate the intersection of two -scapes. Yes, the mediascape is powerful, but it wouldn't exist without the technoscape providing the dissemination technology, the finanscape providing the means for such production/dissemination, the ethnoscape similarly allows media to transport across national and physical boundaries (either because someone's got to transport those papers or because a story/foundational-narrative propagated by media is carried across borders by immigrants), and the ideoscape (if taken in conjunction with Althusser's definition of ideology as the way in which one sees oneself in the world) allows them to identify with these stories, contextualize them (as Lee and LiPuma write, "The circulation of such forms . . . always presupposes the existence of their respective interpretive communities, with their own forms of interpretation and evaluation"). This exercise can be done with any -scape.
So what exactly are -scapes good for? Approximations. The -scapes that have held the most power in Anthropological study inspired by Appardurai have been the ones tracking concrete objects, either commodities or people, across space, connecting them along the way to both the people/systems surrounding them and the Anthropologist's own experience. While the media/techno/ideo-scapes all deal with ideas, things with permeable boundaries always under pressure and threat of de/reconstruction, the corporeal bodies of a human or raw commodity provide some sense of stability (even in the case of cyborgs, which one could argue we all have become, the basic equality of self=body and rules governing the system of human functioning remain constant) provide a basis for exploring these more incorporeal elements creating movement (or, to be more specific and far more dense, the performative combination of movement in time with signification) around these objects and affecting the Anthropologist's own view/discussion of the body. This kind of situationalism/relativism is completely lacking in Appadurai's theory, however, limiting its potential.
Thus ends this week's performance. Sorry for the late start.
(from Wikipedia)
- The partial sums (the Taylor polynomials) of the series can be used as approximations of the entire function. These approximations are good if sufficiently many terms are included.
- The series representation simplifies many mathematical proofs.

Which has an error of about 0.000003. So it's essentially right.
But why exactly would you need it? What's the use in disintegrating a function and letting it dissolve off into infinity? A good number of things, actually. The case above can be used to prove various corollaries of wave theory, often using the Taylor series of cos(x) (which just fills in the missing elements of sin(x)). Other such examples abound.
In a certain sense, this is the very problem Appadurai is attempting to grapple with; since (following Derrida) meaning is infinitely vanishing, infinitely deferred (differentiable?), Appadurai must throw out the concrete notions of space and identity propagated by Anthropology and attempt to factor in movement (which is possibly not even movement at all?). Whatever new function he derives is ineffable, infinite, so it must be broken into parts (an approximation) to be made sense of, to feed in to other theoretical processes and actions. Leading to the -scapes. However, at this point we encounter a new problem: all of these -scapes contain the same origin function. Delineating them as clearly different spaces/fields, as the naming/encapsulating process usually does, quickly becomes a problem when one attempts to locate the intersection of two -scapes. Yes, the mediascape is powerful, but it wouldn't exist without the technoscape providing the dissemination technology, the finanscape providing the means for such production/dissemination, the ethnoscape similarly allows media to transport across national and physical boundaries (either because someone's got to transport those papers or because a story/foundational-narrative propagated by media is carried across borders by immigrants), and the ideoscape (if taken in conjunction with Althusser's definition of ideology as the way in which one sees oneself in the world) allows them to identify with these stories, contextualize them (as Lee and LiPuma write, "The circulation of such forms . . . always presupposes the existence of their respective interpretive communities, with their own forms of interpretation and evaluation"). This exercise can be done with any -scape.
So what exactly are -scapes good for? Approximations. The -scapes that have held the most power in Anthropological study inspired by Appardurai have been the ones tracking concrete objects, either commodities or people, across space, connecting them along the way to both the people/systems surrounding them and the Anthropologist's own experience. While the media/techno/ideo-scapes all deal with ideas, things with permeable boundaries always under pressure and threat of de/reconstruction, the corporeal bodies of a human or raw commodity provide some sense of stability (even in the case of cyborgs, which one could argue we all have become, the basic equality of self=body and rules governing the system of human functioning remain constant) provide a basis for exploring these more incorporeal elements creating movement (or, to be more specific and far more dense, the performative combination of movement in time with signification) around these objects and affecting the Anthropologist's own view/discussion of the body. This kind of situationalism/relativism is completely lacking in Appadurai's theory, however, limiting its potential.
Thus ends this week's performance. Sorry for the late start.
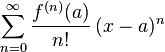
No comments:
Post a Comment